A measure of a fund’s sensitivity to market movements. The beta of the market is 1.00 by definition. Morningstar calculates beta by comparing a fund’s excess return over T-bills to the market's excess return over T-bills, so a beta of 1.10 shows that the fund has performed 10% better than its benchmark index in up markets and 10% worse in down markets, assuming all other factors remain constant. Conversely, a beta of 0.85 indicates that the fund’s excess return is expected to perform 15% worse than the market’s excess return during up markets and 15% better during down markets.
Benefits
Beta can be a useful tool when at least some of a fund’s performance history can be explained by the market as a whole. Beta is particularly appropriate when used to measure the risk of a combined portfolio of mutual funds.
It is important to note that a low beta for a fund does not necessarily imply that the fund has a low level of volatility. A low beta signifies only that the fund’s market-related risk is low. (Standard deviation is a measure of a fund’s absolute volatility.) A specialty fund that invests primarily in gold, for example, will usually have a low beta, as its performance is tied more closely to the price of gold and gold-mining stocks than to the overall stock market. Thus, the specialty fund might fluctuate wildly because of rapid changes in gold prices, but its beta will remain low. R-squared is a necessary statistic to factor into the equation, because it reflects the percentage of a fund’s movements that are explained by movements in its benchmark index.
Origin
All MPT statistics (alpha, beta, and R-squared) are based on a least-squared regression of the fund’s return over T-bills (called excess return) and the excess returns of the fund’s benchmark index. The value of using alpha and beta depends upon the strength of the linear relationship between the fund and the index over the past 36 months. R-squared measures the strength of this relationship. An R-squared of 100, for example, implies a perfect linear relationship, while an R-squared of zero implies that no relationship exists whatsoever. Additionally, the application of MPT statistics (alpha, beta, and R-squared as a group) assumes that beta, which is based on market risk, is the only risk measure necessary.
For the Pros
The formula for beta is as follows:
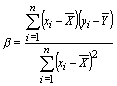
where:
= the mean of the sum of the subsequent equation, from month 1 through month n
n = the number of months
= each x observation (the monthly return of the benchmark index)
= the average of all x observations
= each y observation (the monthly return of the fund)
= the average of all y observations
Investors should keep in mind that beta is a measure of both the upside and downside volatility of a fund relative to its benchmark index, so both greater-than and less-than expected returns are viewed as increased risk.
Also, while beta is a relative (non-absolute) measure, comparisons of beta between different funds can be misleading, because the level of correlation between different funds and the benchmark index (as measured by R-squared) may differ significantly.