The Sharpe Ratio is a risk-adjusted measure developed by Nobel Laureate William Sharpe. It is calculated by using standard deviation and excess return to determine reward per unit of risk. The higher the Sharpe Ratio, the better the portfolio’s historical risk-adjusted performance. It can be used to compare two portfolios directly on how much excess return each portfolio achieved for a certain level of risk.
Origin
Morningstar calculates the Sharpe Ratio on a monthly basis for various time periods.
For the Pros
Morningstar first calculates a monthly Sharpe Ratio and then annualizes it to put the number in a more useful one-year context.
The monthly Sharpe Ratio is:
Sharpe RatioM =
The numerator, average monthly excess return, is the monthly average of the portfolio’s excess return over the risk-free benchmark:
where
= Average monthly excess return of the portfolio
Ri = Return of the portfolio in month i
RFi = Return of the risk-free benchmark in month i
n = Number of months
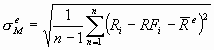
The denominator is the monthly standard deviation of excess returns. Because this measures the standard deviation of the spread between the portfolio and the risk-free rate, it is slightly different than the standard deviation of total returns, as found in most Morningstar products. The monthly standard deviation of excess returns is:
The annualized Sharpe Ratio is the product of the monthly Sharpe Ratio and the square root of 12. This is equivalent to multiplying the numerator by 12 (to produce an arithmetic annualized excess return) and the denominator by the square root of 12 (annualized standard deviation).
Sharpe RatioA = Sharpe RatioM 